[프로그래머스] 정수 삼각형(Java)

문제 풀기

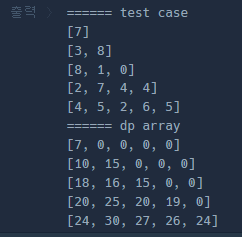
문제 설명

풀이

• DP(Dynamic Programming, 동적 프로그래밍)를 이용하여 해결 가능한 문제
  • 완전 탐색을 이용해서도 해결 가능해 보이지만, 그럴 경우 프로그래머스 효율성 검사에서 걸리지 않을까 싶다.
• 피라미드 꼭대기에서부터 내려오면서, 거칠수 있는 최대값을 기록할 2차원 배열을 사용한다.
• 위에서 생성한 배열을 사용하여, 꼭대기에서 부터 해당 위치까지의 최대값을 기록한다.
• 여기서 윗줄의 값의 경우, 이미 꼭대기에서 부터 모든 최대 경우를 반영하고 있기 때문에 바로 윗줄의 케이스만 고려하면서 값을 채워나가면 된다.

코드

import java.util.*;

class Solution {
    public int solution(int[][] triangle) {
        // dp 배열 초기화
        int[][] dp = new int[triangle.length][triangle.length];
        dp[0][0] = triangle[0][0];

        for (int i = 1; i < triangle.length; i++){
            for (int j = 0; j < triangle[i].length; j++){
                // left: j-1, right: j
                int right = dp[i-1][j];
                int left;
                if (j-1 < 0)    left = right-1; // idx 에러 방지
                else    left = dp[i-1][j-1];
                // dp 갱신
                dp[i][j] = triangle[i][j] + Math.max(left, right);
            }
        }

        // max 탐색
        int max = 0;
        for (int val: dp[triangle.length-1]){
            if (val > max)  max = val;
        }
        return max;
    }
}

실행 결과

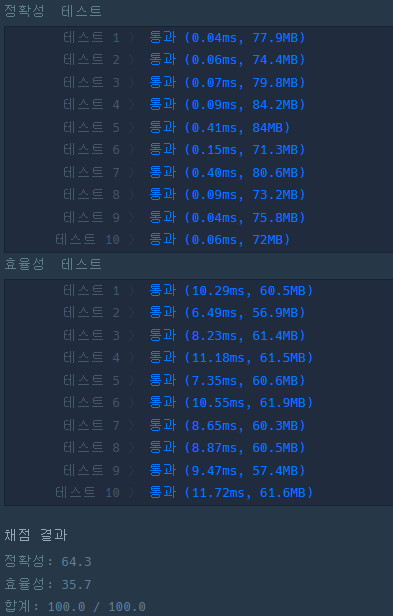
테스트 케이스의 dp 배열 출력 결과